ICPC 2023 南京 VP

I. Counter

操作可以都想成连续的，那么输入 $a,b$，意为在 $a-b$ 处进行了一次归零，之后连着进行了 $b$ 次操作，如果中间有冲突，即为 NO

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl "\n"
#define lowbit(x) ((x)&(-x))
typedef long long ll;
const int N=1e5+7, mod=1e9+7;

void solve(){
    int n,m,flag=0;
    cin>>n>>m;
    map<int,int>vis;
    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        if(b>a)flag=1;
        int l = a - b;
        if(vis.find(l) != vis.end()){
            vis[l] = max(vis[l], a);
        } else {
            vis[l] = a;
        }
    }
    int now=-1;
    for(auto &x:vis){
        if(now>=x.first){
            flag=1;
            break;
        }
        now=x.second;
    }
    cout<<(flag?"No\n":"Yes\n");
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}

C. Primitive Root

通过题上公式可以得到 $g=(kP+1)\oplus(P-1)$

显然 $g$ 的数量就是 $k$ 的个数

异或性质： $a-b\leq a\oplus b\leq a+b$

那么 $0\leq k\leq\left\lfloor\frac mP\right\rfloor-1$ 时，所有的 $k$ 都成立，$k\geq\lceil\frac mP\rceil+1$ 时，所有的 $k$ 都不成立，那么只需要特殊判断两边界之间的值即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl "\n"
#define lowbit(x) ((x)&(-x))
typedef long long ll;
const int N=1e5+7, mod=1e9+7;

ll p,m,ans;

void solve(){
    cin>>p>>m;
    ans=m/p;
    for(ll i=m/p;i<=ceil(1.0*m/p);i++){
        if(((i*p+1)^(p-1))<=m)ans++;
    }
    cout<<ans<<endl;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}

G - Knapsack

显然，免费获取的机会要用在 $w$ 大的物品上

将所有物品排序，先进行一遍背包，得到对前 $i$ 个物品背包时的最大值

再用这个值加上未选的物品中 $v$ 最大的 $k$ 个物品，最大值即为答案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl "\n"
#define lowbit(x) ((x)&(-x))
typedef long long ll;
const int N=1e4+7, mod=1e9+7;

struct Node{
    int w,v;
    bool operator<(const Node &t){
        if(w==t.w)return v<t.v;
        return w<t.w;
    }
}a[N];

ll n,m,k;
ll dp[N][N];

void solve(){
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)cin>>a[i].w>>a[i].v;
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++){
        for(int j=m;j>=0;j--){
            if(j>=a[i].w){
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i].w]+a[i].v);
            }
            else dp[i][j]=dp[i-1][j];
        }
    }
    ll ans=0,sum=0;
    multiset<int>s;
    if(k){
            for(int i=n-k+1;i<=n;i++){
            sum+=a[i].v;
            s.insert(a[i].v);
        }
        ans=dp[n-k][m]+sum;
        for(int i=n-k;i>0;i--){
            if(a[i].v>*s.begin()){
                sum-=*s.begin();
                sum+=a[i].v;;
                s.erase(s.begin());
                s.insert(a[i].v);
            }
            ans=max(ans,dp[i-1][m]+sum);
        }
    }else ans=dp[n][m];
    cout<<ans<<endl;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    // cin>>t;
    while(t--)solve();
    return 0;
}

F - Equivalent Rewriting

每一位的值实际是由最后一次操作他的操作决定的，$n$ 个操作本身构成了 $1~n$ 的拓扑序

只需检查每一位的所有操作，看是否有相邻的操作处于里面，如果有，那么这个 $i \rightarrow i+1$ 这个序列就是不可被更改的，检查完之后如果有没被标记过的即可交换他们的位置，输出即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


#include <bits/stdc++.h>
using namespace std;

const int N=2e6+7;
vector<int> a[N];
int ans[N];
bool vis[N];

void solve(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;++i) {
        ans[i]=i;
        int k;
        cin>>k;
        for(int j=1;j<=k;++j) {
            int x;
            cin>>x;
            a[x].push_back(i);
        }
    }
    for(int i=1;i<=m;++i) {
        if(a[i].empty())  continue;
        int x=a[i].back();
        for(auto y:a[i]) {
            if(y==x-1)  vis[y]=1;
        }
    }
    bool flag=0;
    for(int i=1;i<n;++i) {
        if(!vis[i]) {swap(ans[i],ans[i+1]);flag=1;break;}
    }
    if(!flag)  cout<<"No\n";
    else {
        cout<<"Yes\n";
        for(int i=1;i<=n;++i)  cout<<ans[i]<<" ";
        cout<<"\n";
    }
    for(int i=1;i<=n;++i)  vis[i]=0;
    for(int i=1;i<=m;++i)  a[i].clear();
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}

A - Cool, It’s Yesterday Four Times More

因为 $n*m$ 的数量级很小，可以考虑很暴力的做法

我们可以用一个 $(x,y,i,j)$ 记录位于 $(x,y)$ 的袋鼠能否踢掉位于 $(i,j)$ 的袋鼠，同时易想到位于同一个联通块的袋鼠，能否获胜是一样的

要记录 $(x,y,i,j)$ 不能直接使用 $map$ 来存取，这样会使时间复杂度陡升，要将这 $4$ 个数转换为一个数，从而达到 $O(1)$ 的查询

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl '\n' 
#define lowbit(x) ((x)&(-x))
typedef long long ll;
const int N=1e3+7, mod=1e9+7;

int n,m;
char mp[N][N];
int vis[N*N];
bool flag[N*N];
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};

int gao(int i, int j, int r, int c) { //此处即为转换函数
    return i * m * n * m + j * n * m + r * m + c;
}

void ungao(int msk, int &i, int &j, int &r, int &c) { //此处为还原函数  
    i = msk / (m * n * m);
    j = msk / (n * m) % m;
    r = msk / m % n;
    c = msk % m;
}

bool die(int x,int y){
    return (x<0||y<0||x>=n||y>=m||mp[x][y]=='O');
}

void bfs(int s){
    queue<int>q;
    q.push(s);
    vis[s]=s;
    flag[s]=0;
    while(q.size()){
        int now=q.front();
        q.pop();
        int x,y,a,b;
        ungao(now, x, y, a, b);
        for(int i=0;i<4;i++){
            int xx=x+dx[i],yy=y+dy[i];
            int aa=a+dx[i],bb=b+dy[i];
            if(die(xx,yy))continue;
            if(die(aa,bb)){
                flag[s]=1;
                continue;
            }
            int nxt = gao(xx, yy, aa, bb);
            if(vis[nxt]>=0)continue;
            q.push(nxt);
            vis[nxt]=s;
        }
    }
}

bool check(int x,int y){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(mp[i][j]=='.'){
                if(i==x&&j==y)continue;
                int state = gao(x, y, i, j);
                if(vis[state]==-1)bfs(state);
                if(!flag[vis[state]])return 0;
            }
        }
    }
    return 1;
}

void solve(){
    cin>>n>>m;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)cin>>mp[i][j];
    memset(vis,-1,sizeof(vis));
    memset(flag,0,sizeof(flag));
    int ans=0;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            if(mp[i][j]=='.')ans+=check(i,j);
    cout<<ans<<endl;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}

L - Elevator

偏思维，货物体积只有 $1$ 和 $2$ 这两种情况，可以将体积为 $2$ 的转化为两个体积为 $1$ 的来进行处理

证明如下

如果每一趟都能填满 $k$，那么转化前和转化后的结果相同
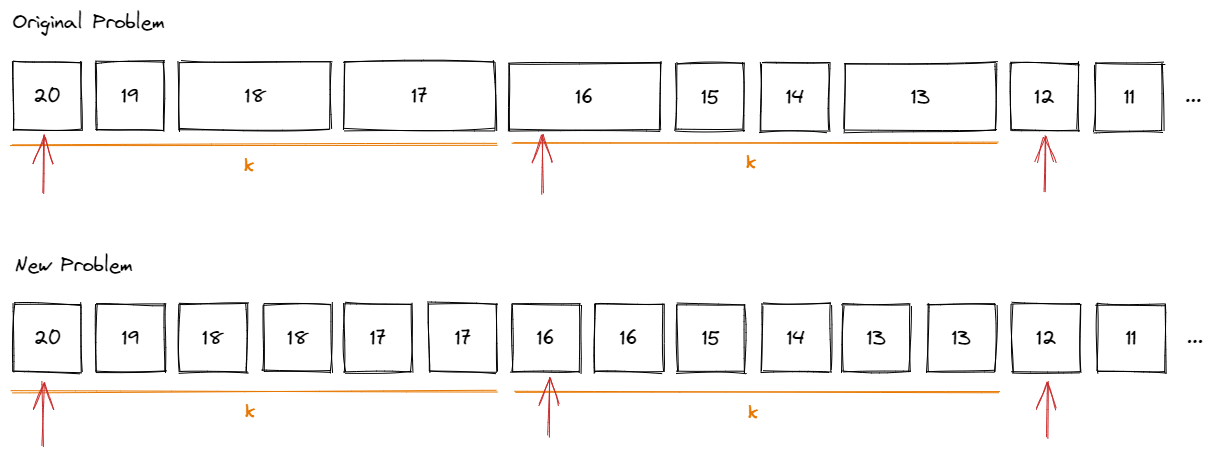
如果出现了剩下体积为 $1$，但是下一个物品体积为 $2$，我们会跳过当前物品，向下寻找体积为 $1$ 的物品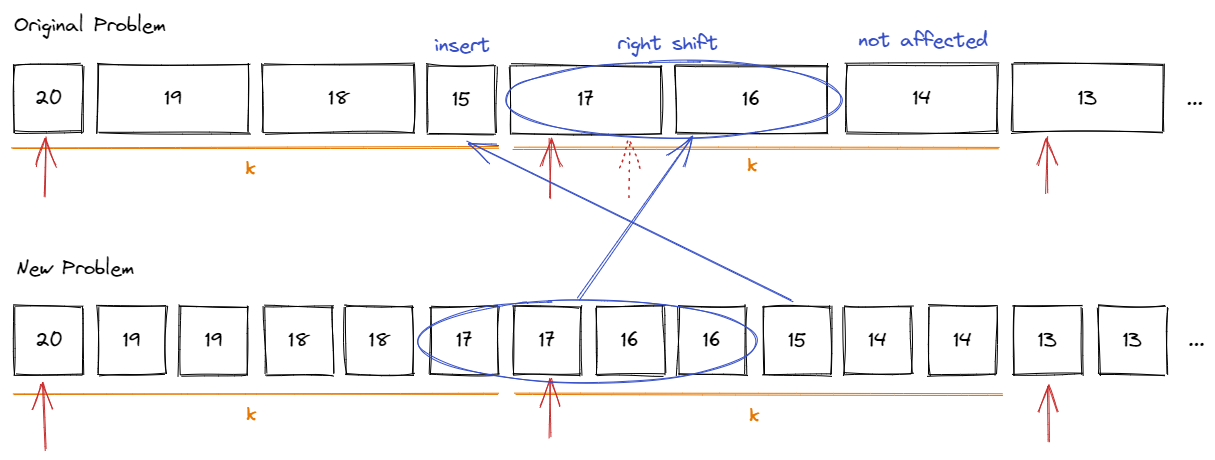由图可知，这样的填充并不会对答案造成影响

所以只需将所有的物品按楼层高度降序排，从高到低每次选够 $k$ 个物品，答案每次加当前最高楼层即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl "\n"
#define lowbit(x) ((x)&(-x))
typedef long long ll;
const int N=1e5+7, mod=1e9+7;

ll n,k;
vector<pair<ll,ll>>w;

void solve(){
    w.clear();
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        ll x,y,z;
        cin>>x>>y>>z;
        w.push_back({z,x*y});
    }
    sort(w.begin(),w.end(),greater<pair<ll,ll>>());
    ll ans=0,now=w[0].first,lst=0;
    for(auto [x,y]:w){
        if(lst){
            if(k>lst+y){
                lst+=y;
                continue;
            }
            y-=(k-lst);
            ans+=now;
            now=x;
            ll t=y/k;
            ans+=now*t;
            lst=y%k;
        }
        else{
            now=x;
            ll t=y/k;
            ans+=t*now;
            lst=y%k;
        }
    }
    if(lst)ans+=now;
    cout<<ans<<endl;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}

M - Trapping Rain Water

根据题目给出的公式格式可以得到 $\sum_{i=1}^nf_i+\sum_{i=1}^ng_i-n\times\max a_i-\sum_{i=1}^na_i$

难点在于如何维护 $\sum_{i=1}^nf_i$ 和 $\sum_{i=1}^ng_i$

$f,g$ 都是单调的序列，可以发现，二者都是连续相同的片段，即片段会以当前片段开头为最大值存在

这样，我们维护这些片段就只需要用 $set$ 来操作即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77


#include <bits/stdc++.h>
using namespace std;
#define ls now<<1
#define rs now<<1|1
#define endl "\n"
#define lowbit(x) ((x)&(-x))
#define pil pair<int,long long>
typedef long long ll;
const int N=1e5+7, mod=1e9+7;
const ll inf=1e18;

int n, q;
ll A[N];
ll fA[N], fsm;
set<pil> fst;
ll gA[N], gsm;
set<pil> gst;

void clear(ll A[], ll &sm, set<pil> &st) {
    memset(A, 0, sizeof(ll) * (n + 3));
    sm = 0;
    st.clear();
    st.insert(pil(1, 0));
    st.insert(pil(n + 1, inf));
}

void update(ll A[], ll &sm, set<pil> &st, int x, ll v) {
    A[x] += v;
    auto it = prev(st.upper_bound(pil(x, inf)));
    if (it->second >= A[x]) return;
    sm -= (next(it)->first - it->first) * it->second;
    sm += (x - it->first) * it->second + (next(it)->first - x) * A[x];
    it = st.insert(pil(x, A[x])).first;
    while (next(it)->second <= A[x]) {
        sm -= (next(it)->first - x) * A[x] + (next(next(it))->first - next(it)->first) * next(it)->second;
        st.erase(next(it));
        sm += (next(it)->first - x) * A[x];
    }
}

void solve() {
    scanf("%d", &n);
    ll mx = 0, sm = 0;
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &A[i]);
        mx = max(mx, A[i]);
        sm += A[i];
    }

    clear(fA, fsm, fst);
    clear(gA, gsm, gst);
    for (int i = 1; i <= n; i++) {
        update(fA, fsm, fst, i, A[i]);
        update(gA, gsm, gst, n + 1 - i, A[i]);
    }

    scanf("%d", &q);
    while (q--) {
        int x, v;
        scanf("%d%d", &x, &v);
        A[x] += v;
        mx = max(mx, A[x]);
        sm += v;
        update(fA, fsm, fst, x, v);
        update(gA, gsm, gst, n + 1 - x, v);
        printf("%lld\n", fsm + gsm - n * mx - sm);
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)solve();
    return 0;
}